Category Archives: Tabular

Tabular models of SQL Server Analysis Services Uses Columnar in-memory storage and DAX
use MDX and DAX as Query Language

Optimizing Columnar Storage for Measures

Posted on by — No Comments ↓

First of all I have to thank Marco Russo for his blog post on Optimizing High Cardinality Columns in Vertipaq and also his great session at SQL PASS Rally Nordic in Stockholm last year which taught me a lot about columnar storage in general. I highly recommend everyone to read the two mentioned resources before continuing here. Most of the ideas presented in this post are based on these concepts and require at least basic knowledge in columnar storage.

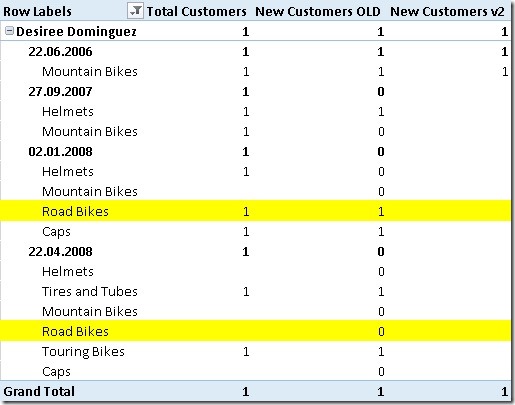
When writing one of my recent posts I ended up with a Power Pivot model with roughly 40M rows. It contained internet logs from Wikipedia, how often someone clicked on a given page per month and how many bytes got downloaded. As you can imagine those values can vary very heavily, especially the amount of bytes downloaded. So in the Power Pivot model we end up having a lot of distinct values in our column that we use for our measure. As you know from Marcos posts, the allocated memory and therefore also the  performance of columnar storage systems is directly related to the number of distinct values in a column – the more the worse. Marco already described an approach to split up a single column with a lot of distinct values into several columns with less distinct values to optimize storage. These concepts can also be used on columns that contain measures or numeric values in general. Splitting numeric values is quite easy, assuming your values range from 1 to 1,000,000 you can split this column into two by dividing the value by 1000 and using MOD 1000 for the second column. Instead of one column with the value 123,456 you end up with two columns with the values 123 and 456. In terms of storage this means that instead of 1,000,000 distinct values we only need to store 2 x 1,000 distinct values. Nothing new so far.

The trick is to combine those columns again at query time to get the original results as before the split. For some aggregations like SUM this is pretty straight forward, others are a bit more tricky. Though, in general the formulas are not really very complex and can be adopted very easily to handle any number of columns:

Aggregation DAX Formula
Value_SUM1 =SUMX(‘1M_Rows_splitted’, [Value_1000] * 1000 + [Value_1])
Value_SUM2 =SUM ( ‘1M_Rows_splitted'[Value_1000] ) * 1000
    + SUM ( ‘1M_Rows_splitted'[Value_1] )
Value_MAX =MAXX(‘1M_Rows_splitted’, [Value_1000] * 1000 + [Value_1])
Value_MIN =MINX(‘1M_Rows_splitted’, [Value_1000] * 1000 + [Value_1])
Value_COUNT =COUNTX(‘1M_Rows_splitted’, [Value_1000] * 1000 + [Value_1])
Value_DISTINCTCOUNT =COUNTROWS (
    SUMMARIZE (
        ‘1M_Rows_splitted’,
        ‘1M_Rows_splitted'[Value_1000],
        ‘1M_Rows_splitted'[Value_1]))

As you can see you can still mimic most kind of aggregation even if the [Value]-column is split up.

Though, don’t exaggerate splitting your columns – too many may be a bit inconvenient to handle and may neglect the effect resulting in worse performance. Marco already showed that you can get a reduction of up to 90% in size, during my simple tests I came up with about the same numbers. Though, it very much depends on the number of distinct values that you actually have in your column!

I would not recommend to always use this approach for all your measure column – no, definitely not! First check how many distinct values your data/measures contain and decide afterwards. For 1 million distinct values it is probably worth it, for 10,000 you may reconsider using this approach. Most important here is to test this pattern with your own data, data model and queries! Test it in terms of size and of course also in terms of performance. It may be faster to split up columns but it may also be slower and it may be also different for each query that you execute against the tabular model / Power Pivot. Again, test with your own data, data model and queries to get representative results! 

Here is a little test that you may run on your own to test this behavior. Simple create the following Power Query using M, load the result into Power Pivot and save the workbook. It basically creates a table with 1 million distinct values (0 to 999,999) and splits this column up into two. You can just copy the workbook, remove the last step “Remove Columns” and save it again to get the “original” workbook and Power Pivot model.

let
    List1 = List.Numbers(0, 1000000),

    TableFromList = Table.FromList(List1, Splitter.SplitByNothing(), null, null, ExtraValues.Error),
    RenamedColumns = Table.RenameColumns(TableFromList,{{"Column1", "Value"}}),
    ChangedType1 = Table.TransformColumnTypes(RenamedColumns,{{"Value", type number}}),
    InsertedCustom = Table.AddColumn(ChangedType1, "Value_1000", each Number.RoundDown([Value] / 1000)),
    InsertedCustom1 = Table.AddColumn(InsertedCustom, "Value_1", each Number.Mod([Value], 1000)),
    ChangedType = Table.TransformColumnTypes(InsertedCustom1,{{"Value_1000", type number}, {"Value_1", type number}}),
    RemovedColumns = Table.RemoveColumns(ChangedType,{"Value"})
in
    RemovedColumns

This is what I ended up with when you compare those two workbooks:

  # distinct values Final Size
single column 1,000,000 14.4 MB
two columns 2 x 1,000 1.4 MB

We also get a reduction in size of 90%! Though, this is a special scenario …
In the real world, taking my previous scenario with the Wikipedia data as an example, I ended up with a reduction to 50%, still very good though. But as you can see the reduction factor varies very much.

Downloads:

Sample workbook with Power Query: 1M_Rows_splitted.xlsx

DAX vs. MDX: DataMembers in Parent-Child Hierarchies

Posted on by — 12 Comments ↓

Recently when browsing the MSDN PowerPivot Forums I came across this thread where the question was ask on how to show the value which is directly linked to an element in a parent-child hierarchy instead of the aggregation of all "children". In this post I am going to address this problem finally showing a proper solution.

 

First of all I would like to start with some background to so called "datamembers". The term "datamember" originates from parent-child hierarchies in multidimensional models. It is a dummy-member that is created automatically below each hierarchy-node to hold values that are linked to a node-member directly. This is of course only possible for parent-child hierarchies.

Take the following MDX-Query for example:

SELECT
[Measures].[Sales Amount Quota] ON 0,
Descendants(
    [Employee].[Employees].&[290],
    1,
    SELF_AND_BEFORE) ON 1
FROM [Adventure Works]
WHERE [Date].[Calendar].[Calendar Year].&[2006]

HiddenDatamember

As we can see, the value of "Amy E. Alberts" is not the Sum of its children but has a difference of $108,000.00 This difference is because of the "datamember" that is also a child of every parent-child node which may be hidden. For multidimensional models his behavior can be changed by setting the MembersWithData-Property to "NonLeafDataVisible":

VSProperties

 

Executing the same query again we now get this results:

VisibleDatamember

Now we see "Amy E. Alberts" twice – the node and the datamember.

 

Doing a similar query on a tabular model we will get this result by default:

q4evw0ne

As you can see, we still have the datamember but without any caption. Though, this can of course be changed when you flatten out the hierarchy using DAX by simply replacing BLANK() by "<my datamember caption>" in your calculated columns.

 

Anyway, this is not the topic of this post but just some background information. Now we will focus on how to query data that is directly associated to a node or its corresponding datamember in MDX and DAX.

 

MDX:

For MDX this is quite easy as the datamember can be referenced by simply using ".datamember" of a given hierarchy node:

WITH

MEMBER [Measures].[DataMember] AS (
[Measures].[Sales Amount Quota],
[Employee].[Employees].currentmember.datamember
), FORMAT_STRING = 'Currency'

SELECT
{
[Measures].[Sales Amount Quota],
[Measures].[DataMember]
} ON 0,
Descendants(
    [Employee].[Employees].&[290],
    1,
    SELF_AND_BEFORE) ON 1
FROM [Adventure Works]
WHERE [Date].[Calendar].[Calendar Year].&[2006]

DatamemberValue_MDX

The DataMember-Measure only shows values that are directly linked to the current node of the parent-child hierarchy. This is pretty straight forward and very easy to accomplish.

 

DAX:

In this DAX this problem is a bit more tricky as we do not have that built-in ".datamember" function. Also navigation within hierarchies and parent-child hierarchies itself are not really supported in DAX. Though, there are several blogs out there that describe how to handle parent-child hierarchies by Alberto Ferrari (here) and Kasper de Jonge (here). Based on these solutions we can create our datamember-calculation.

First (and only) thing we need is to add a calculated column that stores the path depth of the current row. This can be achieved by using this formula:

=PATHLENGTH(
    PATH(
        Employee[EmployeeKey],
        Employee[ParentEmployeeKey]
    )
)

 

Using our previous example and selecting "Amy E. Alberts" together with our new column we get this:

CalculatedColumn_Level

As we can see there are two different Levels below "Amy E. Alberts" where Level=3 holds our datamember-value and Level=4 holds all the other values (=real child members). Lets add a calculated measure to help you make the final calculation more understandable:

MinLevel:=MIN(Employee[Level])

Calculation_MinLevel

So, for our [DataMember]-calculation we simply have to extend the context to only include rows where [Level] = [MinLevel]

DataMember:=CALCULATE(
SUM('Sales Quota'[Sales Amount Quota]),
FILTER('Employee',
    'Employee'[Level] = [MinLevel]))

CalculationNotWorking_DAX

Well, obviously our calculation is not returning the expected results. This is because of a very common pitfall which I am also very prone to. Whenever a calculated measure is used within an other calculated measure, a CALCULATE() gets wrapped around it thereby taking over the current context. In our case this means that ‘Employee'[Level] will always be the same as [MinLevel] as [MinLevel] gets evaluated for each row and doing MIN() on only one row of course always returns the value of the current row which we compared it to!

To solve this issue we have to place the original [MinLevel]-calculation directly into our [DataMember]-calculation:

DataMember:=CALCULATE(
SUM('Sales Quota'[Sales Amount Quota]),
FILTER('Employee',
    'Employee'[Level] = MIN(Employee[Level])))

CalculationWorking_DAX

This change finally makes the calculation return the correct results also when browsing using the hierarchy:

DatamemberValue_DAX

 

Even though DAX is not very good in handling hierarchies, the [DataMember]-calculation can be accomplished quite easily. This calculation also works for hierarchies of any depth without needing to adopt it. In terms of performance it may be further improved to the following formula – though the impact will be minor:

DataMember_v2:=CALCULATE(
SUM('Sales Quota'[Sales Amount Quota]),
FILTER(VALUES('Employee'[Level]),
    'Employee'[Level] = MIN(Employee[Level])))

 

Download Final Model (Office 2013!)

Universal Quantiles Calculation for PowerPivot using DAX

Posted on by — 10 Comments ↓

In my last post I showed a new approach on how to calculate the median in PowerPivot using DAX. In the comments the question was raised whether it is possible to make that calculation universal for all kind of Quantiles like Median, Quartiles, Percentiles, etc. and that’s what this post is about.

Lets analyze the final Median calculation from the last post:

Median SA Months:=CALCULATE([SumSA],
TOPN(
2-MOD([Cnt_Months], 2),
TOPN(
([Cnt_Months] + 1) / 2,
VALUES(‘Date’[Month]),
[SumSA]),
[SumSA],
1))
/
(2-MOD([Cnt_Months], 2))

 

The Median defines the value in the middle of an ordered set. To get the first half (+1 to handle even and odd sets) of the whole we are using TOPN function:

TOPN(
([Cnt_Months] + 1) / 2,
VALUES(‘Date’[Month]),
[SumSA]),

The important part here is the “divide by 2” to split the set in the middle to start our Median calculation. Instead of dividing by 2 we could also multiply by 0.5 where 0.5 would be the separator for our quantile (in this case the Median). This expression can be made dynamic. For the first Quartile we would use 0.25 for the second Quartile (=Median) we would use 0.5 and for the third Quartile we would use 0.75.

I created a little linked table to demonstrate the dynamic approach:

Quantile SortOrder Percentage
Median 1 0.5000
Quartile 1 401 0.2500
Quartile 2 402 0.5000
Quartile 3 403 0.7500
Sextile 1 601 0.1667
Sextile 2 602 0.3333
Sextile 3 603 0.5000
Sextile 4 604 0.6667
Sextile 5 605 0.8333

We also need to add a calculated measure that returns the percentage-value of the currently selected Quantile:

SelectedQuantile:=IF(
HASONEVALUE(Quantiles[Percentage]),
VALUES(Quantiles[Percentage]))

 

Now we can change our old Median-calculation to be dynamic by using the measure defined above:

Quantile SA Months:=CALCULATE([SumSA],
TOPN(
2 – MOD([Cnt_Months], 2),
TOPN(
ROUNDUP(([Cnt_Months] + 1) * [SelectedQuantile], 0),
VALUES(‘Date’[Month]),
[SumSA]),
[SumSA],
1))
/
(2 – MOD([Cnt_Months], 2))

We also need to explicitly add ROUNDUP() as “([Cnt_Months] + 1) * [SelectedQuantile]” may return any decimal places whereas the previous divide by 2 could only result in a x.5 which was rounded up automatically. And well, that’s all we need to change in order to make the calculation universal for all different Quantiles! The rest is the same logic that I already described for Median calculation.

 

Download Final Model (Office 2013!)

Calculating Median in PowerPivot using DAX

Posted on by — 23 Comments ↓

I just came across this blog post by Bill Anton where he discusses several approaches to calculated the Median of a given set in T-SQL, MDX and DAX. In the end of his post when it comes to the DAX calculation, he references several post by Marco, Alberto and Javier (post1, post2) that already address that kind of calculation in DAX. But he also claims that non of the solutions is “elegant”. Well, reason enough for me to try it on my own and here is what I came up with. Its up to you to decide whether this solution is more elegant than the others or not 🙂

In general, the median calculation always varies depending on the number of items and whether this number is even or odd.
For an even population the median is the mean of the values in the middle:
the median of {3, 5, 7, 9} is is (5 + 7)/2 = 6
For an odd population, the median is the value in the middle:
the median of {3, 5, 9} is 5

In both cases the values have to be ordered before the calculation. Note that it does not make a difference whether the values are sorted in ascending or descending order.

OrderedValues

In this example, our set contains 12 items (=months) so we have to find the 2 items in the middle of the ordered set – December and February – and calculate the mean.

So, how can we address this problem using DAX? Most of the posts I mentioned above use some kind of combination of ranking – RANKX() – and filtering – FILTER(). For my approach I will use none of these but use TOPN instead (yes, I really like that function as you probably know if you followed my blog for some time).

In this special case, TOPN() can do both, ranking and filtering for us. But first of all we need to know how many items exist in our set:

Cnt_Months:=DISTINCTCOUNT(‘Date’[Month])

 

This value will be subsequently used in our next calculations.

To find the value(s) in the middle I use TOPN() twice, first to get the first half of the items (similar to TopCount) and then a second time to get the last values that we need for our median calculation (similar to BottomCount):

TopBottom

As the median calculation is different for even and odd sets, this also has to be considered in our calculation. For both calculations MOD()-function is used to distinguish both cases:

Items_TopCount:=IF(MOD([Cnt_Months],2) = 0,
([Cnt_Months] / 2) + 1,
([Cnt_Months] + 1) / 2)

For an even number of items (e.g. 12) we simply divide the count of items by 2 and add 1 which gives us a (12 / 2) + 1 = 7 for our sample.
For an odd number of items (e.g. 5) we first add 1 to our count of items and then divide by 2 which gives us (5 + 1) / 2 = 3

Items_BottomCount:=IF(MOD([Cnt_Months],2) = 0, 2, 1)

For an even number of items we have to consider the last 2 values whereas for an odd number of items we only have to consider the last value.

 

These calculations are then used in our median calculation:

Median SA Months:=CALCULATE([SumSA],
TOPN(
[Items_BottomCount],
TOPN(
[Items_TopCount],
VALUES(‘Date’[Month]),
[SumSA]),
[SumSA] * -1))
/
[Items_BottomCount]

As DAX has no built-in BOTTOMN()-function, we need to “abuse” the TOPN() function and multiply the OrderBy-value by “–1” to get the BOTTOMN() functionality. As you can see most of the logic is already handled by our [Items_TopCount] and [Items_BottomCount] measures and this pattern can be reused very easily.

 

Of course all these calculations can also be combined and the use of IF() can be avoided:

Median SA Months v2:=CALCULATE([SumSA],
TOPN(
2 – MOD([Cnt_Months], 2),
TOPN(
([Cnt_Months] + 1) / 2,
VALUES(‘Date’[Month]),
[SumSA]),
[SumSA] * -1))
/
(2 – MOD([Cnt_Months], 2))

Note: for an even population ([Cnt_Months] + 1) / 2 returns X.5 which is automatically rounded up when it is used in a function that expects a whole number. In our example this is what happens: (12 + 1) / 2 = 6.5 –> 7

These are the final results:

FinalResults

 

Additional content:

We could also use AVERAGEX() to calculate our median but I think that it is some kind of overhead to use AVERAGEX() just to divide by “1” or “2” depending on the number of items that our TOPN-functions return:

Median SA Months AvgX:=AVERAGEX(
TOPN(
2-MOD([Cnt_Months], 2),
TOPN(
([Cnt_Months] +1) / 2,
VALUES(‘Date’[Month]),
[SumSA]),
[SumSA] * -1),
[SumSA])

 

As you can see there are various approaches to calculate the median, its up to you which on you like most. I have not tested any of them in terms of performance over bigger sets – this may be topic for an upcoming post.

 

Download Final Model (Office 2013!)

Another Post about Calculating New and Returning Customers – Part 2

Posted on by — 3 Comments ↓

In my previous post I showed a new approach on how to calculate new (and returning) customers in PowerPivot/tabular using DAX. We ended up with a solution where we added the customers first order date as a calculated column to our customer-table. This column was then linked to our date-table with an inactive relationship. The final calculation used USERELATIONSHIP() to make use of this relationship as follows:

New Customers:=CALCULATE(
COUNTROWS(Customer),
USERELATIONSHIP(Customer[FirstOrderDate], ‘Date’[Date]))

This calculation performs really well as it does not have to touch the fact-table to get the count of new customers. And this is also the issue with the calculation as other filters are not reflected in the calculation:

Issue_Old_vs_New

Take row 2 as an example: we have 8 “Total Customers” of which 12 are “New Customers”. Obviously an error in the calculation. The PivotTable is filtered to Category=”Road Bikes” and we have 8 customers on the 2nd of February that bought a road bike. The “New Customers” calculation on the other hand is not related to the Subcategory and shows 12 as in total there were 12 new customers for all products.

 

To get our calculation working also with other filters we have to somehow relate it to our fact-table. So far we calculated the customers first order date only in the customer table. The customers first order may be related to several fact-rows, e.g. one row for each product the customer bought. Our “New Customers” calculation should only include customers that are active considering also all other filters.

To identify a customers first order in our fact-table we can again use a calculated column and also re-use our previous calculated column in our Customer-table that holds the customers first order date:

=NOT(
ISBLANK(
LOOKUPVALUE(
Customer[CustomerKey],
Customer[CustomerKey],
[CustomerKey],
Customer[FirstOrderDate],
[Order Date]
)))

This returns True for all fact-rows associated with a customers first order and False for all other rows.

The final “New Customers v2” calculation is quite simple then – in addition to the active filters we add a further filter to only select rows that are associated to a customers first order:

New Customers v2:=CALCULATE(
[Total Customers],
‘Internet Sales’[IsCustomersFirstOrder] = TRUE())

 

And this are the results:

Final_Old_vs_NewV2

As you can see there are still differences between “New Customers OLD” and “New Customers v2”. But is this really a problem with the new calculation? Lets analyze the issue taking customer “Desiree Dominguez” where we encounter the first difference as an example:

Issue_Analyzed

“Desiree Dominguez” had her first order on the 22th of June in 2006. So she is actually no “new customer” in 2008. The reason why the old calculation counts her as “new customer” is that it was the first time that she bought a product of subcategory “Road Bikes”. Whether this is correct or not is up to your business definition of a “new customer”. According to my experience it is more likely that “Desiree Dominguez” is not counted as a new customer in 2008 and so the “New Customer v2” actually returns the more accurate results.

 

Additional stuff:

An other option for this calculation is to rank the [Order Date] or [Sales Order Number] for each customer within the fact-table using the calculation below:

=RANKX(
FILTER(
ALL(‘Internet Sales’),
[CustomerKey] = EARLIER([CustomerKey])),
[Order Date],
[Order Date],
1,
DENSE
)

[Order Date] could be replaced by [Sales Order Number]. This makes sense if a customer can have multiple orders per day and you also want to distinguish further by [Sales Order Number]. The new field would also allow new analysis. For example the increase/decrease in sales from the second order compared to the first order and so on.

The “New Customer” calculation in this case would still be similar. We just have to filter on the new calculated column instead:

New Customers v3:=CALCULATE(
[Total Customers],
‘Internet Sales’[CustomersOrderNr] = 1)

 

Download Final Model (Office 2013!)

 

 

The multidimensional model:

The whole logic of extending the fact-table to identify rows that can be associated with a customers first order can also be used in a multidimensional model. Once we prepared the fact-table accordingly the calculations are quite easy. The biggest issues here does not reside in the multidimensional model itself but in the ETL/relational layer as this kind of operation can be quite complex – or better say time-consuming in terms of ETL time.

At this point I will not focus on the necessary ETL steps but start with an already prepared fact-table and highlight the extensions that have to be made in the multidimensional model. The fact-table already got extended by a new column called [IsCustomersFirstOrder] similar to the one we created in tabular using a DAX calculated column. It has a value of 1 for rows associated with a customers first order and 0 for all other rows.

The next thing we have to do is to create a new table in our DSV to base our new dimension on. For simplicity I used this named query:

MD_NamedQuery_Dim

This table is then joined to the new fact-table:

MD_DSV

The new dimension is quite simple as it only contains one attribute:

MD_Dimension

You may hide the whole dimension in the end as it may only be used to calculate our “new customers” and nowhere else and may only confuse the end-user.

 

Once we have added the dimension also to our cube we can create a new calculated measure to calculate our “new customers” as follows:

CREATE MEMBER CURRENTCUBE.[Measures].[New Customers] AS (
[Measures].[Customer Count],
[Is Customers First Order].[Is Customers First Order].&[1]
), ASSOCIATED_MEASURE_GROUP = ‘Internet Customers’
, FORMAT_STRING = ‘#,##0’;

The calculation is based on the existing [Customer Count]-measure which uses DistinctCount-aggregation. Similar to DAX with just extend the calculation by further limiting the cube-space where “Is customers First Order” = 1.

This approach also allows you to create aggregations if necessary to further improve performance. So this is probably also the best way in terms of query-performance to calculate the count of new customers in a multidimensional model.

Another Post about Calculating New and Returning Customers

Posted on by — 5 Comments ↓

I know, this topic has already been addressed by quite a lot of people. Chris Webb blogged about it here(PowerPivot/DAX) and here(SSAS/MDX), Javier Guillén here, Alberto Ferrari mentions it in his video here and also PowerPivotPro blogged about it here. Still I think that there are some more things to say about it. In this post I will review the whole problem and come up with a new approach on how to solve this issue for both, tabular and multidimensional models with the best possible performance I could think of (hope I am not exaggerating here  🙂 )

OK, lets face the problem of calculating new customers first and define what a new customer for a given period actually is:

A new customer in Period X is a customer that has sales in Period X but did not have any other sales ever before. If Period X spans several smaller time periods
(e.g. Period X=January contains 31 days) then there must not be any sales before the earliest smaller time period (before 1st of January) for this customer to be counted as a new customer.

According to this definition the common approach can be divided into 2 steps:
1) find all customers that have sales till the last day in the selected period
2) subtract the number of customers that have sales till the day before the first day in the
selected period

 

First of all we need to create a measure that calculates our distinct customers.
For tabular it may be a simple calculated measure on your fact-table:

Total Customers:=DISTINCTCOUNT(‘Internet Sales’[CustomerKey])

For multidimensional models it should be a physical distinct count measure in your fact-table, ideally in a separate measure group.

How to solve 1) in tabular models

This is also straight forward as DAX has built-in functions that can do aggregation from the beginning of time. We use MAX(‘Date’[Date]) to get the last day in the current filter context:

Customers Till Now:=CALCULATE(
[Total Customers],
DATESBETWEEN(
‘Date’[Date],
BLANK(),
MAX(‘Date’[Date])))

 

 

How to solve 2) in tabular models

This is actually the same calculation as above, we only use MIN to get the first day in the current filter context and also subtractt “1” to get the day before the first day.

Previous Customers:=CALCULATE(
[Total Customers],
DATESBETWEEN(
‘Date’[Date],
BLANK(),
MIN(‘Date’[Date])-1))

 

To calculate our new customers we can simply subtract those two values:

New Customers OLD:=[Customers Till Now]-[Previous Customers]

 

 

How to solve 1) + 2) in multidimensional models

Please refer to Chris Webb’s blog here. The solution is pure MDX and is based on a combination of the range-operator “{null:[Date].[Calendar].currentmember}”, NONEMPTY() and COUNT().

 

 

Well, so far nothing new.

 

So lets describe the solution that I came up with. It is based on a different approach. To make the approach easily understandable, we have to rephrase the answer to our original question “What are new customers”?”:

A new customer in Period X is a customer that has his first sales in Period X.

According to this new definition we again have 2 steps:
1) Find the first date with sales for each customer
2) count the customers that had their first sales in the selected period

I will focus on tabular models. For multidimensional models most of the following steps have to be solved during ETL.

 

How to solve 1) in tabular models

This is pretty easy, we can simply create a calculated column in our Customer-table and get the first date on which the customer had sales:

=CALCULATE(MIN(‘Internet Sales’[Order Date]))

 

How to solve 2) in tabular models

The above create calculated column allows us to relate our ‘Date’-table directly to our ‘Customer’-table. As there is already an existing relationship between those tables via ‘Internet Sales’ we have to create an inactive relationship at this point:

Customer_Date_Relationship

Using this new relationship we can very easy calculate customers that had their first sales in the selected period:

New Customers:=CALCULATE(
COUNTROWS(Customer),
USERELATIONSHIP(Customer[FirstOrderDate], ‘Date’[Date]))

 

Pretty neat, isn’t it?
We can use COUNTROWS() opposed to a distinct count measure as our ‘Customer’-table only contains unique customers – so we can count each row in the current filter context.
Another nice thing is that we do not have to use any Time-Intelligence function like DATESBETWEEN which are usually resolved using FILTER that would iterate over the whole table. Further it also works with all columns of our ‘Date’-table, no matter whether it is [Calendar Year], [Fiscal Semester] or [Day Name of Week]. (Have you ever wondered how many new customers you acquired on Tuesdays? 🙂 )   And finally, using USERELATIONSHIP allows us to use the full power of xVelocity as native relationships are resolved there.

 

The results are of course the same as for [New Customers OLD]:

Result_Old_vs_New

 

Though, there are still some issues with this calculation if there are filters on other tables:

Issue_Old_vs_New

As you can see, our new [New Customers] measure does not work in this situation as it is only related to our ‘Date’-table but not to ‘Product’.

I will address this issue in a follow-up post where I will also show how the final solution can be used for multidimensional models – Stay tuned!

Download Final Model (Office 2013!)

 

UPDATE: Part2 can be found here

Fiscal Periods, Tabular Models and Time-Intelligence

Posted on by — 12 Comments ↓

I recently had to build a tabular model for a financial application and I would like to share my findings on this topic in this post. Financial applications tend to have “Periods” instead of dates, months, etc. Though, those Periods are usually tied to months – e.g. January = “Period01”, February = “Period02” and so on. In addition to those “monthly periods” there are usually also further periods like “Period13”, “Period14” etc. to store manually booked values that are necessary for closing a fiscal year. To get the years closing value (for a P&L account) you have to add up all periods (Period01 to Period14). In DAX this is usually done by using TOTALYTD() or any similar Time-Intelligence Function.

 

Here is what we want to achieve in the end. The final model should allow the End-user to create a report like this:

DesiredResult

This model allows us to analyze data by Year, by Month and of course also by Period. As you can see also the YTD is calculated correctly using DAX’s built-in Time-Intelligence functions.

However, to make use of Time-Intelligence functions a Date-table is required (more information: Time Intelligence Functions in DAX) but this will be covered later. Lets start off with a basic model without a Date-table.

For testing purposes I created this simple PowerPivot model:

BaseModel 

Sample of table ‘Facts’:

AccountID PeriodID Value
4 201201

41,155.59
2 201201

374,930.01
3 201211

525,545.15
5 201211

140,440.40
1 201212

16,514.36
5 201212

639,998.94
3 201213

-100,000.00
4 201213

20,000.00
5 201214

500,000.00

 

 

The first thing we need to do is to add a Date-table. This table should follow these rules:
– granularity=day –> one row for each date
– no gaps between the dates –> a contiguous range of dates
– do not use use the fact-table as your date-table –> always use an independent date-table
– the table must contain a column with the data type “Date” with unique values
– “Mark as Date-table”

A Date-table can be created using several approaches:
– Linked Table
– SQL view/table
– Azure Datamarket (e.g. Boyan Penev’s DateStream)
– …

(Creating an appropriate Date-table is not part of this post – for simplicity i used a Linked Table from my Excel workbook).

I further created calculated columns for Year, Month and MonthOfYear.

 

At this point we cannot link this table to our facts. We first have to create some kind of mapping between Periods and “real dates”. I decided to create a separate table for this purpose that links one Period to one Date. (Note: You may also put the whole logic into a calculated column of your fact-table.) This logic is straight forward for periods 1 to 11 which are simply mapped to the last (or first) date in that period. For Periods 12 and later this is a bit more tricky as we have to ensure that these periods are in the right order to be make our Time-Intelligence functions work correctly. So Period12 has to be before Period13, Period13 has to be before Period14, etc.

So I mapped Period16 (my sample has 16 Periods) to the 31st of December – the last date in the year as this is also the last period. Period 15 is mapped to the 30th of December – the second to last date. And so on, ending with Period12 mapped to the 27th of December:

PeriodID Date
201101 01/31/2011
201102 02/28/2011
201111 11/30/2011
201112 12/27/2011
201113 12/28/2011
201114 12/29/2011
201115 12/30/2011
201116 12/31/2011
201201 01/31/2012
201202 02/29/2012

I called the table ‘MapPeriodDate’.

This table is then added to the model and linked to our already existing Period-table (Note: The table could also be linked to the Facts-table directly using PeriodID). This allows us to create a new calculated column in our Facts-table to get the mapping-date for the current Period:

=RELATED(MapPeriodDate[Date])

 

The new column can now be used to link our Facts-table to our Date-Table:

FinalModel

Please take care in which direction you create the relationship between ‘Periods’ and ‘MapPeriodDate’ as otherwise the RELATED()-function may not work!

Once the Facts-table and the Date-table are connected you may consider hiding the unnecessary tables ‘Periods’ and ‘MapPeriodDate’ as all queries should now use the Date-table. Also the Date-column should be hidden so the lowest level of our Date-table should be [Period].

 

To get a [Period]-column in our Date-table we have to create some more calculated columns:

[Period_LookUp]
= LOOKUPVALUE(MapPeriodDate[PeriodID], MapPeriodDate[Date], [Date])

this returns the PeriodID if the current date also exists in the MapPeriodDate-table. Note that we only get a value for the last date in a month.

 

[Period]
= CALCULATE(MIN([Period_LookUp]), DATESBETWEEN('Date'[Date], [Date], BLANK()))

our final [Period]-calculation returns the first populated value of [Period_LookUp] after the current date. The first populated value for dates in January is the 31st which has a value of 201101 – our PeriodID!

 

The last step is to create our YTD-measures. This is now very easy as we can again use the built-in Time-Intelligence functions with this new Date-table:

ValueYTD:=TOTALYTD(SUM([Value]), 'Date'[Date])

And of course also all other Time-Intelligence functions now work out of the box:

ValuePYTD:=CALCULATE([ValueYTD], DATEADD('Date'[Date], –1, YEAR))

 

All those calculations work with Years, Months and also Periods and offer the same flexibility that you are used to from the original financial application.

 

Download Final Model (Office 2013!)

Dynamic ABC Analysis in PowerPivot using DAX

Posted on by — 46 Comments ↓

An ABC Analysis is a very common requirement for for business users. It classifies e.g. Items, Products or Customers into groups based on their sales and how much impact they had on the cumulated overall sales. This is done in several steps.

I just published a new version of the Dynamic ABC Analysis at www.daxpatterns.com. The article can be found here.

 

1) Order products by their sales in descending order
2) Cumulate the sales beginning with the best selling product till the current product
3) Calculate the percentage of the cumulated sales vs. total sales
4) Assign a Class according to the cumulated percentage

Marco Russo already blogged about this here. He does the classification in a calculated column based on the overall sales of each product. As calculated columns are processed when the data is loaded, this is not dynamic in terms of your filters that you may apply in the final report. If, for example, a customer was within Class A regarding total sales but had no sales last year then a report for last year that uses this classification may give you misleading results.

In this blog I will show how to do this kind of calculation on-the-fly always in the context of the current filters. I am using Adventure Works DW 2008 R2 (download) as my sample data and create a dynamic ABC analysis of the products.

The first thing we notice is that our product table is a slowly changing dimension of type 2 and there are several entries for the same product as every change is traced in the same table.

SCD2Table

So we want to do our classification on the ProductAlternateKey (=Business Key) column instead of our ProductKey (=Surrogate Key) column.

First we have to create a ranking of our products:

Rank CurrentProducts:=IF(HASONEVALUE(DimProduct[ProductAlternateKey]),
IF(NOT(ISBLANK([SUM SA])),
RANKX(
CALCULATETABLE(
VALUES(DimProduct[ProductAlternateKey]),
ALL(DimProduct[ProductAlternateKey])),
[SUM SA])))

Check if there is only one product in the current context and that this product also has sales. If this is the case we calculate our rank. We need to do the CALCULATETABLE to do the ranking within the currently applied filters on other columns of the DimProduct-table e.g. if a filter is applied to DimProduct[ProductSubcategoryKey] we want to see our ranking within that selected Subcategory and not against all Products.

I also created a measure [SUM SA] just to simplify the following expressions:

SUM SA:=SUM(FactInternetSales[SalesAmount])

 

The second step is to create a running total starting with the best-selling product/the product with the lowest rank:

CumSA CurrentProducts:=SUMX(
TOPN(
[Rank CurrentProducts],
CALCULATETABLE(
VALUES(DimProduct[ProductAlternateKey]),
ALL(DimProduct[ProductAlternateKey])),
[SUM SA]),
[SUM SA])

We use a combination of SUMX() and TOPN() here. TOPN() returns the top products ordered by [SUM SA]. Further we use our previously calculated rank to only get the products that have the same or more sales than the current product. For example if the current product has rank 3 we sum up the top 3 products to get our cumulated sum (=sum of the first 3 products) for this product. Again we need to use CALCULATETABLE() to retain other filters on the DimProduct-table.

 

The third step is pretty easy – we need to calculate percentage of the cumulated sales vs. the total sales:

CumSA% CurrentProducts:=
[CumSA CurrentProducts]
/
CALCULATE([SUM SA], ALL(DimProduct[ProductAlternateKey]))

This calculation is straight forward and should not need any further explanation.

The result of those calculations can be seen here:

Theory

 

To do our final classification we have to extend our model with a new table that holds our classes and their border-values:

Class LowerBoundary UpperBoundary
A 0 0.7
B 0.7 0.9
C 0.9 1

Class A should contain products which’s cumulated sales are between 0 and 0.7 – between 0% and 70%.
Class B should contain products which’s cumulated sales are between 0.7 and 0.9 – between 70% and 90%.
etc.

(This table can later be extended to support any number of classes and any boundaries between 0% and 100%.)

To get the boundaries of the selected class we create two measures that are later used in our final calculation:

MinLowerBoundary:=MIN([LowerBoundary])
MaxUpperBoundary:=MAX([UpperBoundary])

 

Our final calculation looks like this:

SA Classified Current:=IF(NOT(ISCROSSFILTERED(Classification[Class])),
[SUM SA],
CALCULATE(
[SUM SA],
FILTER(
VALUES(DimProduct[ProductAlternateKey]),
[MinLowerBoundary] < [CumSA% CurrentProducts]
&& [CumSA% CurrentProducts] <= [MaxUpperBoundary])))

If our Classification-table is not filtered, we just show our [SUM SA]-measure. Otherwise we extend the filter on our DimProduct[ProductAlternateKey] using our classification filtering out all products that do not fall within the borders of the currently selected class.

This measure allows us to see the changes of the classification of a specific product e.g. over time:

FinalResults_1

In 2006 our selected product was in Class C. For 2007 and 2008 it improved and is now in Class A. Still, overall it resides in Class B.

We may also analyze the impact of our promotions on the sales of our classified products:

FinalResults_2

Our Promotion “Touring-1000 Promotion” only had impact on products in Class C so we may consider to stop that promotion and invest more into the other promotions that affect all classes.

 

The classification can be used everywhere you need it – in the filter, on rows or on columns, even slicers work. The only drawback is that the on-the-fly calculation can take quite some time. If I find some time in the future i may try to further tune them and update this blog-post.

 

The example workbook can be downloaded here:

Though it is already in Office 2013 format an may not be opened with any previous versions of Excel/PowerPivot.
It also includes a second set of calculations that use the same logic as described above but does all the calculations without retaining any filters on the DimProducts-table. This allows you to filter on Class “A” and ProductSubcategory “Bike Racks” realizing that “Bike Racks” are not a Class “A” product or to see which Subcategories or Categories actually contain Class A, B or C products!

Relationships on columns with non-unique values and how to tune them

Posted on by — 2 Comments ↓

If you follow my blog frequently, you may have realized that in many of them I cover scenarios where I need to create relationships on columns with non-unique values. For example when handling SCD2 facts and dimensions or dealing with parallel hierarchies. In all the examples I use a combination of FILTER– and CONTAINS-function to create those non-unique relationships between tables. Recently I ran into performance issues using this approach and was thinking about on how to tune those kind of "relationships".

First of all I was taking a look at the DAX Query Plan using SQL Server Profiler to get some more information on what’s going on inside xVelocity and DAX. I used an calculation from my previous post as an example:

Value_Sender:=
CALCULATE([Value_SUM],
FILTER(
     'Facts',
     CONTAINS(
          'Sender',
          'Sender'[SenderID],
          'Facts'[SenderID]))
)

We had to use this calculation as SenderID was not unique in our Sender-table (and of course also not in our Facts-table). When we tried to create a relationship we got the error

Error

"The relationship cannot be created because each column contains duplicate values. Select at least one column that contains only unique values."

This makes absolutely sense as tabular models natively only support 1:n / n:1 relationships and therefore at least one column has to contain only unique vales.

The calculation from above using FILTER and CONTAINS still allowed us to link our tables on those non-unique column values. The drawback of the calculation is that it may not perform very well as it cannot use the full power of xVelocity that heavily relies on predefined relationships between columns and tables. But in our case we create the relationship on-the-fly not using xVelocity’s full potential. Further, by using CONTAINS, which is not a native xVelocity-function, the engine has to callback to DAX formula engine as we can see in the profiler:

VertiPaq SE Query / 0 – VertiPaq Scan (8 times of which 4 are of subclass Internal)

VertiPaq_SE_Query_CONTAINS

[CallbackDataID(….)] is always an indicator that the xVelocity engine could not resolve the query on its own but had to call functions from the DAX formula engine as Jeffrey Wang described here. This in the end results in poor query performance (at least compared to a pure xVelocity query).

DAX Query Plan / 1 – DAX VertiPaq Logical Plan (just for sake of completeness)

QueryPlan_CONTAINS

 

So the key to tune those kind of relationships is to relate the tables at design time to get full xVelocity performance at query time. As the tables cannot be related directly, we have to add an intermediate table containing only unique values – in our case unique SenderIDs. This table can then be used to create 1:n relationships with our Sender and our Facts table

SenderID
TOT
EUROPE
GER
FR
NA
USA
CAN
EXTERNAL
TOT_2
JV
HOLD

If you are using a SQL database as datasource you can simply create a view using SELECT DISTINCT or write the select statement directly in PowerPivot.

Once the table has been added we can create relationships as shown below:

Relationships

This design is similar to a many-to-many design with the only difference that we combined our intermediate table and our bridge table into one single table. The rest is similar to resolving many-to-many relationship as I described here. So once we have created these relationships we can change our calculations as follows:

Value_Sender_Bridge:=
CALCULATE(
     [Value_SUM],
     'SenderBridge',
     'Sender'
)

This calculation can be resolved by the xVelocity engine without any callbacks to DAX formula engine. Taking a look at the profiler trace proves this:

VertiPaq SE Query / 0 – VertiPaq Scan (4 times of which 2 are of subclass Internal)

VertiPaq_SE_Query_CROSSTABLE

None of the Veripaq SE queries used [CallbackDataID(….)] or any other complex function. Only joins have been used which can be handled by the xVelocity engine very easily:

DAX Query Plan / 1 – DAX VertiPaq Logical Plan (just for sake of completeness)

QueryPlan_CROSSTABLE

Also the logical plan could be drastically simplified containing only Sum_Vertipaq and Scan_Vertipaq operators telling us that the query can be executed in pure Vertiscan mode.

Details on Vertipaq operators and Vertiscan mode can be found here.

 

 

I have not run a lot of tests on bigger tables yet where I could have compared the overall performance but this may follow in a later post. With this post I just wanted to show how to link tables on columns containing non-unique values.

It would be great if tabular models would support those kind of relationships out of the box and that you can create them like any other relationships using drag&drop in the diagram view. This would have made many of my previous workshops at customers much easier Smile.

Consolidation and Intercompany Elimination with parallel hierarchies

Posted on by — 2 Comments ↓

In my last post I described and approach on how to calculate consolidated values (adjusted by intercompany eliminations) using PowerPivot and DAX. In this post I will extend this technique so it can also be used with parallel hierarchies as this is also very common in financial applications.

Switching from a single hierarchy to multiple parallel hierarchies has several drawbacks for tabular models:
1) business keys cannot be used to build the PC-hierarchy as they are not unique anymore
2) artificial keys and parent-keys are required
3) as business keys are not unique anymore, we also cannot create a relationship between facts and our dimension
4) PowerPivot tables do not support “UNION” to load several single hierarchies and combine them

All the issues described above have to be handled before the hierarchies can be loaded into PowerPivot. This is usually done in a relational database but this will not be covered in this post.

For simplicity I created a table in Excel that already has the correct format:

IDParentIDSenderIDName
1 TOTMy Whole Company by Region
21EUROPEEurope
32GERGermany Company
42FRFrench Company
51NANorth America
65USAUS Company
75CANCanadian Company
-99 EXTERNALEXTERNAL
8 TOT_2My Whole Company Legal View
98JVJoint Ventures
109FRFrench Company
119USAUS Company
128HOLDMy cool Holding
1312GERGermany Company
1412CANCanadian Company

We have 2 parallel hierarchies – “My Whole Company by Region” and “My Whole Company Legal View”. In PowerPivot this looks like this:

Each Company can be assigned to different nodes in every hierarchy.

As I already noted above, the SenderIDs are not unique anymore, and therefore we cannot create a relationship to our fact-table. So we have to handle this in our calculation. The approach is similar to handling SCD2 dimensions in PowerPivot what I described in previous posts (Part1 and Part2). We use CONTAINS-function to filter our fact-table based on the currently active SenderIDs in the dimension-table:

Value_Sender:=
CALCULATE([Value_SUM],
FILTER(
     'Facts',
     CONTAINS(
          'Sender',
          'Sender'[SenderID],
          'Facts'[SenderID]))
)

Actually this is the only difference in the calculation when we are dealing with multiple parallel hierarches. The other calculations are the same with the only difference that we have to use [Value_Sender] instead of [Value_SUM]:

Value_Internal:=
 CALCULATE([Value_Sender],
 FILTER(
      'Facts',
      CONTAINS(
           'Sender',
           'Sender'[SenderID],
           'Facts'[ReceiverID]))
 )

and

Value_External:=
 CALCULATE([Value_Sender],
 FILTER(
      'Facts',
      NOT(
           CONTAINS(
                'Sender',
                'Sender'[SenderID],
                'Facts'[ReceiverID])))
 )

As you can see this approach also works very well with multiple hierarchies. In the end we get the desired results:

Taking a look at “My cool Holding” we see that a value of 50 is eliminated as there have been sales from CAN to GER. On top-level of the hierarchy we see the same values being eliminated (170) as both hierarchies contain the same companies and therefore only sales to EXTERNAL can summed up to get the correct value.

As this technique operates on leaf-level it works with all possible hierarchies regardless of how many companies are assigned to which node or how deep the hierarchies are!

(Just to compare the values from above – the fact-table is the same as in the previous post: )

SenderIDReceiverIDValue
FRGER100
CANGER50
GEREXTERNAL70
USACAN30
USAFR10
USAEXTERNAL90
CANUSA50
CANEXTERNAL10